蒙特卡罗法（Monte Carlo method）是一种使用统计概率的方法来解决问题的一个思路。

这个统计概率的方法可以是传统的频度论的统计概率，也可以是贝叶斯理论、贝叶斯统计。

蒙特卡罗法的基本思想比较简单，举个圆周率π的例。

假设不知道π的值，现在要求π。

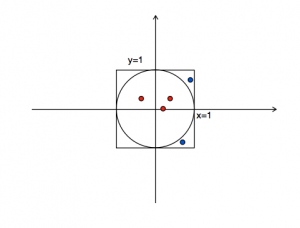
从图中已知：圆的半径为1。所以通过面积公式 S=π*r^2　就可以知道 S(圆)=π 。

同样，正方形的面积也可以知道为 S(正)=2*2=4 。

既然知道了正方形和圆的面积，那么圆比正方形就可以明白了。 圆:正=π:4=pi/4

接下来，按照蒙特卡罗法的思路来求pi。

基本的蒙特卡罗法的思路就是：
1，生成随机数；
2，计算随机数；
3，反复计算（为了更精确）。

随机生成m个座标点，图中蓝色的点为位于圆外、正方形内的随机座标（n个），红色为圆内。

那么，用概率论的思想来说，生成的m个点中，落入圆内的概率p就是 P=n/m 。

这个概率应该是等于圆与正方形面积比的，所以可以知道

π/4=n/m

那么，就可以求出

π=4n/m
（考虑到精确度，m的值越大，求出来的π也就越精确。）
程序列：

以上就是蒙特卡罗法的基本思路。（顺便一说：例子里面，判断随机点是否为圆内可以用到(0,0)的距离是否大于半径来做判断之类等等。）

通常蒙特·卡罗方法通过构造符合一定规则的随机数来解决数学上的各种问题。对于那些由于计算过于复杂而难以得到解析解或者根本没有解析解的问题，蒙特·卡罗方法是一种有效的求出数值解的方法。一般蒙特·卡罗方法在数学中最常见的应用就是蒙特·卡罗积分。

另外，随着理论的发展出现了很多蒙特卡罗法的“变异体”，这些“变异体”对蒙特卡罗法做了调整从而使得计算速度更高、结果更加精确。

@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@

如果使用贝叶斯理论

贝叶斯理论的关键，在于生成的随机点位于圆内的概率，使用的是事后概率。

P(H|D)=[P(D|H)*P(H)]/P(D)

所以，如果使用贝叶斯的理论那么就应该是

π/4=P(H|D)

π=4*P(H|D)

这个方法的好处在于计算的过程是反复更新的，因为随着点的增多，P(H|D)也会趋向于频度论的最终收束值。

其次，由于贝叶斯理论的思考过程类似于人脑的思维模式，所以在解决一些决策或者正在调研中的问题的时候可以使用贝叶斯理论。

这样子，结果可以随着试验次数的增加而越来越精确，等同于是把一套复杂的试验给分解了。